下面进行关于弹簧吸收存储的能量。
(a)线性特性吸收存储的能量
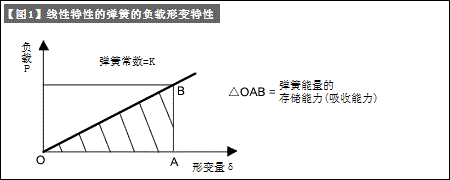
弹簧受到负载后,根据胡克定律,产生形变(【图1】)。当弹簧受到载荷时,根据胡克定律(图1)产生挠曲(形变)。 如果从这个状态快速松开负载,弹簧会震荡恢复到原来的状态。 因此,在负载状态下,弹簧因形变而累积能量。
这种弹簧存储的能量用下列表达式来表达。
弹簧存储的能量U = k ・δ2 / 2 k:弹簧常数 δ:形变量 |
这个表达式相当于【图1】中三角形OAB的面积。
如果把【图1】中三角形OAB面积的大小认为是弹簧能量存储的能力的话,那么以下说法也成立。
* 相同弹簧的存储能量,形变量越大,存储的能量越大。
* 不同的弹簧,即使弹簧常数小,形变量大也能获得相当量的能量存储。
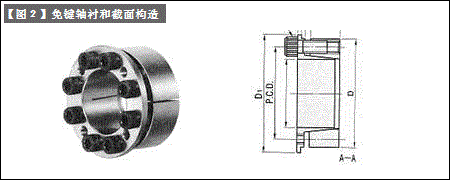
这方面的例子包括精密仪器减震器和免键轴衬【图2】。
(b)非线性特性的弹簧吸收存储的能量
・根据弹簧的构造,弹簧形变时会吸收存储能量。
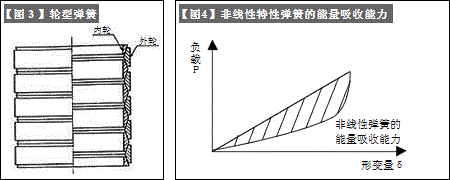
・轮型弹簧(【图3】)是由具有圆锥面的结构的内轮和外轮交叉重叠的弹簧,在轴的方向施加作用力时,内轮和外轮的圆锥面产生摩擦力。因为这个摩擦力吸收了一部分由形变产生的能量,所以经常被应用在缓冲装置(参考【图4】)。
・【图4】所示,一次形变所吸收的能量相当于【图4】中负载-形变曲线所包围的面积。
下一讲,我们关于弹簧的固有振动进行解说。