让我们来练习使用欧拉公式进行顶出销屈曲的相关强度计算。
问题
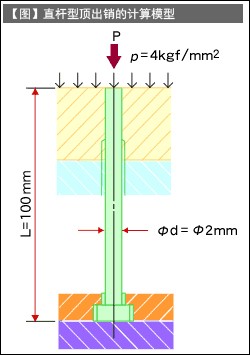
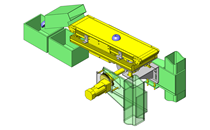
请对【图】中所示直杆型顶出销的屈曲强度进行研判。
|
|
解答例
根据图,
顶出销的直径 | φd | = | φ2(mm) | |
全长 | l | = | 100(mm) | |
SKH51的弹性模量 | e | = | 21000(kgf/mm2) | |
取决于终端条件的常熟 | n | = | 4 | |
截面惯性半径 | k | = | d/4 | |
= | 2/4 | |||
= | 0.5(mm) | |||
因此,根据欧拉公式,屈曲荷载P为
P | =nπ2AE(K/L)2 | |
=4×π2 ×(π×2 2 /4)×21000×(0.5/100)2 | ||
=65(kgf) |
另一方面,作用于顶出销的压缩荷载P1为
P1 | =p×A | |
=p×(π×d2/4) | ||
=4×(π×22/4) | ||
=12.6(kgf) |
安全系数S | = | P/P1 |
= | 65/12.6 | |
= | 5.2 |
∴ 根据经验可以判定,安全系数取5.2即可确保足够的屈曲强度。