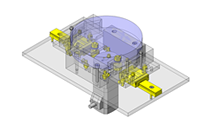
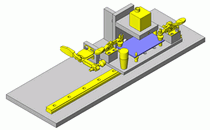
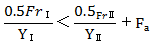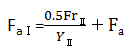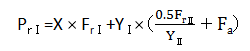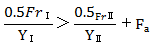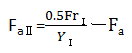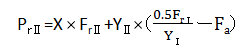球轴承的问题之一是因疲劳导致达到使用寿命。本期栏目中,将通过一个具体的案例来讲解如何预测这一问题。
· 球轴承劣化的机理
· 施加在球轴承上的静载荷
· 施加在球轴承上的动载荷
球轴承劣化的机理
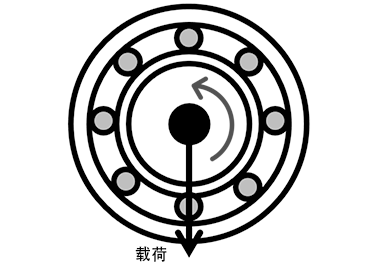
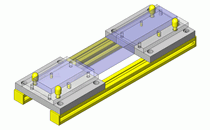
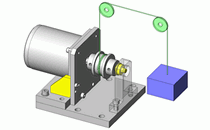
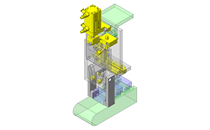
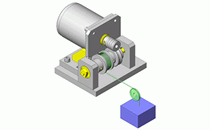
当旋转体重量等载荷作为轴承载荷作用于轴承时,由于滚动体与内圈外圈之间的摩擦损耗,会导致内圈和外圈磨损,从而发生球轴承的劣化。旋转体所负载的载荷,根据其作用方法不同,可以如图1所示分为2种类型。
图1.施加在球轴承上的外力
※外圈:固定、固定在固定座上 内圈:旋转、固定在旋转轴上
载荷方向不变的类型 | 载荷方向变化的类型 |
|
|
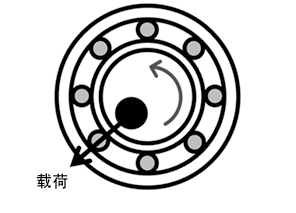
因旋转体的自重(静态)而相对于轴的旋转产生的载荷始终在一个方向上。 | 由于旋转体的不平衡(动态),载荷会随着轴的旋转而旋转。 |
包括载荷方向不因旋转轴的旋转而改变的类型,以及因旋转体不平衡导致载荷方向发生改变的情况。无论哪种情况,在内圈的滚动面与滚动体之间、滚动体与外圈的滚动面之间所产生的载荷都是不断发生改变的重复载荷,而反复变化的载荷会引发疲劳。轴承的寿命可由支撑载荷乘以转数得到的数值确定,可作为总转数计算出来。对于球轴承所负载的载荷,用户必须考虑以下2点。
表1.施加在球轴承上的外力
分类 | 内容 | 判定 |
静态 | 停止或低速旋转时负载载荷 | 基本额定静载荷 |
动态 | 决定旋转寿命的负载载荷 | 基本额定动载荷 |
为了提高轴承负载载荷、延长寿命,可采用大于这一数值的球轴承,在设计时可作如下选择。
①轴承的滚动体尺寸增大,进行该操作时轴承的形状也会变大。
②通过将滚动体由钢球改为滚子,相当于将深沟球轴承改为圆柱滚子轴承。
表2表示将这一载荷产品目录值的“基本额定静载荷*1”和“基本额定动载荷*1 ”施加在内径为φ20的球轴承上时的情况。
提示
*1 即使是相同种类、相同尺寸的滚动轴承,这种载荷也会因制造商等而异,因此用户应通过产品目录等渠道获取要使用的轴承的数据并应用于设计中。
表2.球轴承基本额定动载荷和基本额定静载荷的参考值
种类 | JIS公称 | 内径×外形×宽 | 基本额定动载荷 | 基本额定静载荷 |
深沟球轴承 | 6004 | φ20×φ42×12 | 9.85 | 5.05 |
6204 | φ20×φ47×14 | 12.79 | 6.66 | |
6304 | φ20×φ52×15 | 15.9 | 7.89 | |
圆柱滚子轴承 | NU204ET | φ20×φ47×14 | 25.69 | 22.64 |
NJ2204ET | φ20×φ52×15 | 29.52 | 27.48 |
对不同型号轴承产品的基本额定动载荷、圆柱滚子轴承 的额定动载荷进行对比,则可一目了然。圆柱滚子轴承的额定动载荷达到深沟轴承的2倍以上。可以看出,滚子的线接触比钢珠的点接触具有更高的接触应力缓和能力。表3中总结了这些额定载荷的含义。
表3.滚珠轴承基本额定动载荷和基本额定静载荷值的内容
项目 | 内容 |
基本额定静载荷 | 是指在停止或以极低速旋转时,会在滚动体与内外圈之间产生相当于滚动体直径0.0001倍的永久变形的应力载荷,对于滚动轴承为4,200MPa(428kg/mm2),对于滚子轴承为4,000MPa(408kg/mm2) |
基本额定动载荷 | 总转数达到100万转时,相同形状的滚动轴承中的90%不会发生疲劳寿命的载荷 |
在进行滚珠轴承选型时,如果负载载荷与寿命存在问题,则必须根据这两个数字计算出对应的该值。在此,由于负载载荷取决于基本额定静载荷,因此必须在该值以下使用。必须根据所施加载荷的种类评估负载载荷。
施加在球轴承上的静载荷
当将静载荷称为“基本当量静载荷”时,是根据使用条件,按照经验确定的系数来估测该载荷的占比。当系数取“S”时,滚动球轴承和滚动滚子轴承的S值如下所示。可以施加到用户关注的旋转体上的载荷就是基本当量静载荷,其计算方法如下。
基本当量静载荷=基本额定静载荷/系数
表4.基本额定静载荷的系数
S(最小值) | 条件 | |
滚珠轴承 | 滚子轴承 | |
2 | 3 | 静音旋转(平稳旋转) |
1 | 1.5 | 普通旋转(平稳旋转) |
1.5 | 3 | 冲击载荷 |
计算施加在轴承上的载荷时,可能需要按照直角坐标系的标准,将其分解为半径方向(径向、r方向)和轴方向(轴向、a方向),以考虑需要支撑的载荷。体现这一思路的手段,就是“径向当量静载荷”。
径向当量静载荷由以下两个公式表示,取二者中较大的数值作为径向当量静载荷(Por)的设计值。
1. 径向当量静载荷(Por)=0.6 x 径向载荷(Fr)+ 0.5 x 轴向载荷(Fa)
2. 径向当量静载荷(Por)=径向载荷(Fr)
施加在球轴承上的动载荷
另一方面,作为动态问题的疲劳寿命总转数的计算方法如下所示。疲劳寿命是在实验公式中融合了经验知识,以如下公式表示。总转数可通过“基本额定动载荷”和由用户设计的旋转体形状确定的“当量动载荷”确定。在进行该计算时,如上所述,是由用户确定的当量动载荷,而这一滚珠轴承的寿命计算公式是一个实验公式,当量动载荷中也融入了经验知识和取决于滚珠轴承几何形状的数值,因此在确定当量动载荷时必须将这些因素考虑在内。
滚珠轴承疲劳寿命计算公式
1. 滚珠轴承:L=(C/P)3 × 106 转 2. 滚子轴承:L=(C/P)3 × 1010/3 转
| L:额定寿命 C:基本额定动载荷(kgf) 径向轴承:Cr P:当量动载荷N(kgf) 径向轴承:Pr |
根据载荷种类进行的修正
必须根据载荷的种类相应乘以系数来修正施加在轴承上的载荷。修正表如表5所示。
轴承负载载荷 =(修正系数)x(通过几何计算和运动计算得出的轴承载荷)
表5.轴承负载载荷的修正表
冲击的种类 | 补正系数 | 机械案例 |
基本无冲击时 | 1.0~1.2 | 电气设备、机床、仪器仪表类 |
存在较轻冲击时 | 1.2~1.5 | 铁道车辆、汽车、轧钢机、金属机械、造纸机械、印刷机械、飞机、纺织机械、电子设备、办公设备 |
存在强烈冲击时 | 1.5~3.0 | 破碎机、工业机械、建筑机械、起重机械 |
角接触球轴承的载荷计算
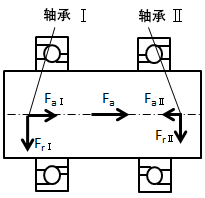
图2.角接触球轴承的受力作用
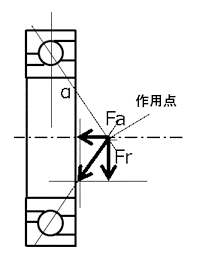
对于轴承具有接触角(α)的角接触球轴承和圆锥滚子轴承,当承受径向载荷时,由于其几何形状而在轴向方向上产生的分力大小按照如下公式计算得出。
轴向分力 (Fa) = 0.5 × 径向载荷 (Fr) / 轴向载荷系数 (Y)
Fa,Fr的单位:
N(kgf)
表6显示了角接触球轴承的力的作用,这是本计算示例的基础。由接触角α可以判断出,从径向载荷Fr产生了轴向方向上的载荷。按照如下方式计算径向载荷和轴向载荷。虽然此处省略了具体的计算示例和X、Y修正系数的概念,但请理解施加在轴承上的载荷可以通过分解为轴向、径向分力而计算出来。
表6.角接触球轴承载荷条件下的径向当量动载荷计算案例
轴承安装 | 载荷条件 | 轴向载荷 | 径向当量动载荷 |
|
|
|
|
- |
| ||
| - |
| |
|
|
米思米 | 米思米 |
米思米 | 米思米 | 米思米 | 米思米 |
米思米 | 米思米 | ||
关联类别
· 球轴承
· 滚子轴承
· 陶瓷轴承
· 轴承组件
关联内容