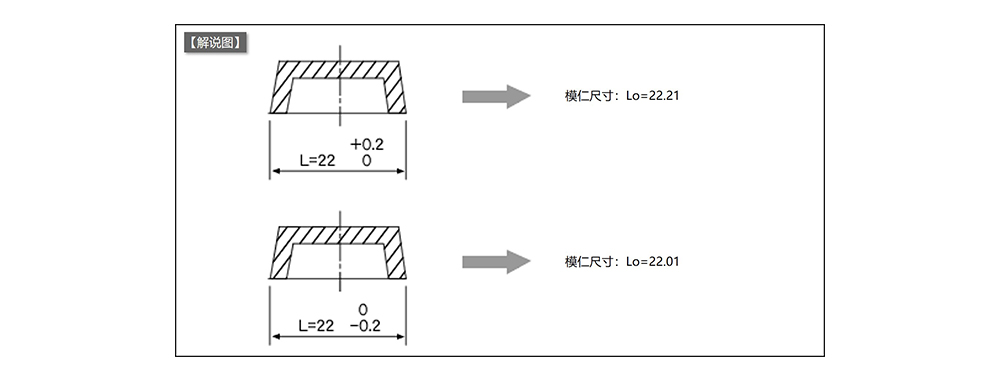
应用例1:成形品尺寸公差为单边公差的场合(非±公差的场合)
举成形品的尺寸公差为22的场合为例。
失败例)Lo=(1+α)×L
=(1+0.005)×22
=1.005×22
=22.11
根据这个计算结果来制作模仁的话,相当于成形品的偏差概率按+方向、-方向同样的分布概率在考虑,如果发生比预测更大收缩率的场合,超过了一侧公差时就发生危险。
因此,像这样的单侧公差的情况,需针对公差中心的收缩来计算。
适合的案例)Lo=(1+α)×L
=(1+0.005)×(22+(0.2/2))
=1.005×22.1
=22.21
应用例2:成形品尺寸公差为单边公差的场合(非±公差的场合)
同样举成形品的尺寸公差为22的场合为例。
失败例)Lo=(1+α)×L
=(1+0.005)×22
=1.005×22
=22.11
根据这个计算结果来制作模仁的话,和前一个例子同样,发生比预想收缩小的情况,同样会超出+侧的公差发生危险。
因此,在这种情况下,也需要针对公差中心的收缩来计算。
适合的案例)Lo=(1+α)×L
=(1+0.005)×(22-(0.2/2))
=1.005×21.9
=22.01
像这样,对不同成形品的尺寸公差,来决定合适的模仁的尺寸。