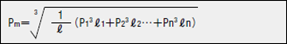● 载荷计算
线性系统是在支撑物体重量的同时进行直线往复运动,所以其所承受的载荷会因物体的重心位置、推力作用位置或是起动停止以及加速、减速的速度变化等因素而发生变化。在进行线性系统选型时,务必充分考虑这些条件。
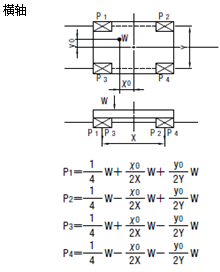
表-5 使用条件与载荷计算公式
分类 | 使用条件与载荷 | 分类 | 使用条件与载荷 | |
1 |
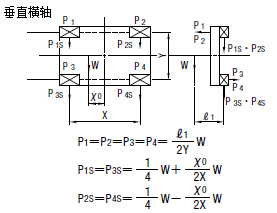
| 3 |
| |
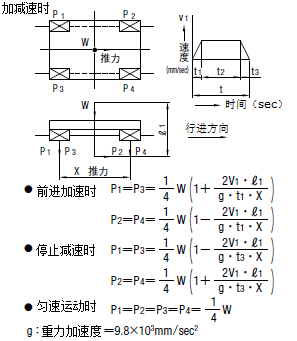
4 |
| |||
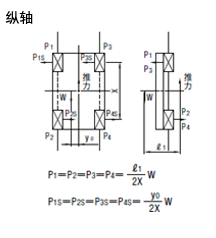
2 |
|
W :作用载荷(N) X、Y :线性系统的跨距(mm) t1 :加速时间(sec) | V :移动速度(mm/sec) P1、P2、P3、P4:线性系统承受的载荷(N) t3:减速时间(sec) |
● 变动载荷的等效载荷
作用于线性系统的载荷,会因其使用方法不同而出现各种变化。例如,往复运动的起动、停止时,以及匀速运动时,在传送时还需要考虑是否有工件等。对于这种变动载荷,在计算使用寿命时必须计算出等效载荷,以确保寿命与该条件下的寿命相等。
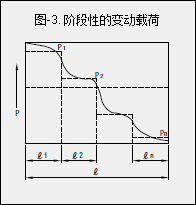
① 载荷根据距离而呈现阶段性变化时(图-3)
承受载荷P1,行走距离ℓ1 通过下式计算出等效载荷Pm。
Pm:变动载荷的等效载荷(N) ℓ : 总行走距离(m)
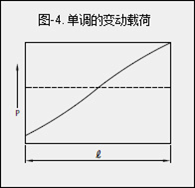
| ② 载荷基本呈线性变化时(图-4)
等效载荷Pm可通过下式近似地求出。
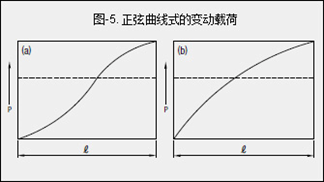
· Pmin:变动载荷的最小值(N) · Pmax:变动载荷的最大值(N) ③ 载荷如图-5(a)、(b)所示按照正弦曲线变化时
等效载荷Pm可通过下式近似地求出。
|
直线导轨
额定寿命是指,让一组相同的直线导轨在同等条件下分别运行时,其中的90%未发生剥落的情况下达成的总行走距离。 额定寿命可根据基本额定动载荷与直线导轨承受的载荷,利用如下公式计算得出。
L :额定寿命(km) C :基本额定动载荷(N) fT :温度系数(参阅图-2) P :作用载荷(N) fw :载荷系数(参阅表-4) | 使用寿命时间可通过计算单位时间内的行走距离计算得出。当行程长度与行程次数一定时,可通过以下公式求出。
Lh :使用寿命(hr) ℓs :行程长度(m) L : 额定寿命(km)n1 :毎分钟往复次数(cpm) |
线性滑道
线性滑道的额定载荷取决于滚动体(滚柱数量),是根据下表计算得出。
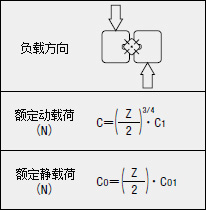
使用1轴
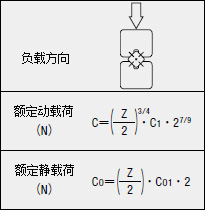
| 纵向使用1轴
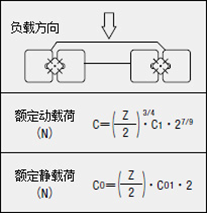
| 2轴并列使用
|
C1: 每个滚轮的基本额定动载荷(N)
Co1: 每个滚轮的基本额定静载荷(N)
Z : 滚动体数量
线性滑道的寿命是根据下式计算得出。
L :寿命(km) fT :温度系数(参阅图-2) fw :载荷系数(参阅表-4) C :额定动载荷(N) P :作用载荷(N) | 寿命时间
Lh :使用寿命(hr) L :寿命(km) ℓs :行程长度(m) n1 :毎分钟往复次数(cPm)
|