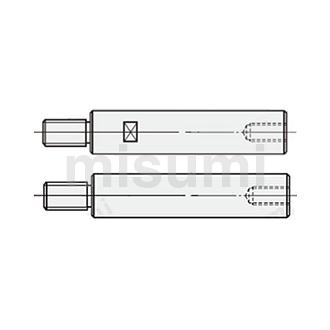
在注塑成型模具的结构中,经常会有将有圆柱或棱柱形零件组合成柱状使用的情况。例如,支撑柱、顶出销、直推管、斜顶杆等。
力会作用于柱的顶端,这是可以预期到的,但众所周知,当力作用于柱上时,会因为难以仅仅依靠弯曲应力或压缩应力予以解释的现象而损坏。这种由于作用在柱尖部分的力而引发损坏的现象称为屈曲。
柱的长度越长,则发生的屈曲越显著。此外,柱的末端是固定的还是处于可以自由移动的状态,也会让屈曲发生的方式发生改变。
屈曲会在何种状态下发生,已经通过许多实验在一定程度上做了力学上的解读。可以通过材料力学计算来预测屈曲的发生。然后,通过对屈曲进行力学计算,可以预测出合适的支柱粗细、顶出销发生屈曲的风险等。
在屈曲计算中提出了以下理论:
1. 戈登-兰金经验公式(Gordon Rankin's formula)
2. 台特迈尔压杆稳定性公式(Tetmajer's formula)
3. 约翰逊方程(Johnson's equation)
4. Southwell公式
5. ω法
6. Engesser修正公式
7. 卡尔曼公式(Kalman's formula)
8. Shanley切线模量理论
这些理论只能在有限的范围和前提条件下适用,如果希望了解更多详情,需要通过研读材料力学方面的书籍进行学习。在力学计算中,是通过许多破坏性实验的积累实现理论化,因此在应用计算公式前必须充分了解实验的前提条件等。在不明确的状态下将计算出的结果应用到模型设计中非常危险的,所以如果想更深入地了解,仔细阅读专业书籍是一条捷径。
目前,利用Excel等计算软件可以很方便的作图和图表化,但是了解计算公式是如何推导出来的、充分了解其背景,是成为一流模具设计师的必要条件。