作为滚珠轴承寿命要点的旋转体自重所导致的载荷中,施加在滚珠轴承上的部分已在从零件重量了解轴承寿命的计算示例(寿命预测)中做了说明。在本期中,主要对具体的计算方法以及重心位置的计算方法进行讲解。
· 关于寿命计算模型
· 步骤1:计算旋转体(零件①+②)的重量与重心位置
· 步骤2:计算因旋转零部件②而对旋转体施加的离心力
· 步骤3:计算轴承的当量动载荷
· 步骤4:计算轴承寿命
关于寿命计算模型
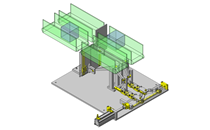
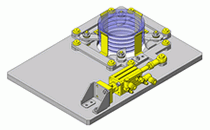
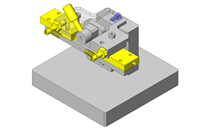
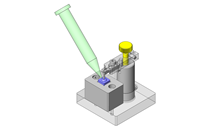
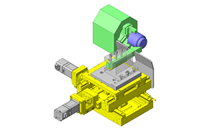
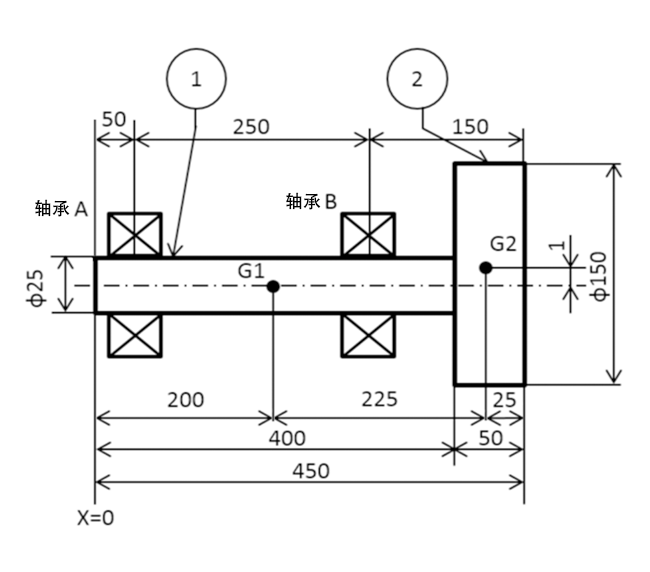
按照上述步骤,计算由图1所示的滚珠轴承(6005 型)支撑,以1mm的偏心量安装在旋转体①上的旋转零部件②以1,500rpm的速度旋转时的轴承寿命。施加在轴承上的载荷的修正系数为1。
图 1.计算案例模型
※使用轴承6005 10.1kN(基本额定动载荷)
当施加径向载荷和推力载荷时,由于这两种载荷而作用在轴承中心且具有同等寿命的虚拟载荷称为当量动载荷。在本案例中,将径向载荷视为当量动载荷。
步骤1:计算旋转体(零件①+②)的重量与重心位置
表 1
部件 | 形状 | 质量(kg) | 重心位置(mm) | 质量(kg)×重心位置(mm) |
① | φ25 × 400 | 1.532 | 200 | 306.4 |
② | φ150 × 50 | 6.892 | 425 | 2929.1 |
模型整体合计 | 8.424 | 384.1 | 3235.5 | |
重心位置=3236/8.42=384.1mm
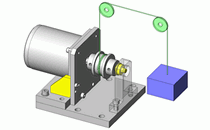
步骤2:计算旋转零部件②对旋转体施加的离心力
因旋转不平衡而产生的离心力F作用于半径方向(详情将在图3中说明),可通过下式计算出来。
F=mrω2
在此,各种符号的含义如下所示。
F:离心力(N(= kg·m/s2)) m:质量(kg)=6.89 r:偏心半径(m)=0.001 ω:角速度(rad/s) |
计算示例中,2 × π × 1500rpm/60s=2 × π × 25 ,带入公式中可得
F=mrω2=6.89 × 0.001 × (2 × π × 25)2=170N
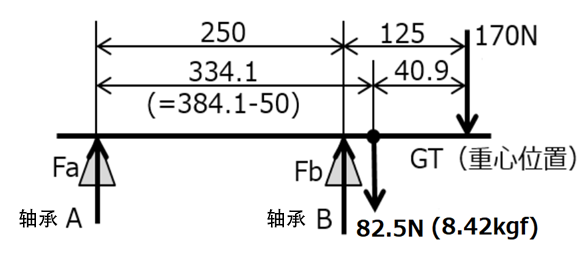
图2.旋转体的当量载荷图
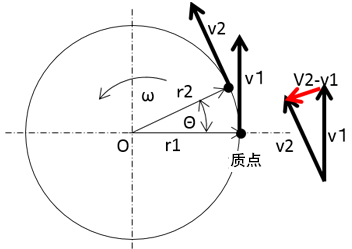
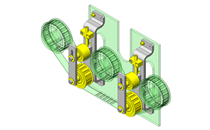
关于离心能力
图3.离心力说明
| 有一个质点在以O为圆心、半径r的圆周上沿CCW(逆时针)方向以角速度ω作匀速圆周运动。 |
步骤3:计算轴承的当量动载荷
a)施加在重心上的力分配给轴承
由于有82.5N的力是施加在重心上的力,因此不会产生力矩,所以施加在轴承A和B上的力可以通过以下方程组计算得出。
平行力:Fag + Fbg = 82.5 力矩力:Fag × 334.1 + Fbg × (125-40.9) = 0 |
求解该方程组得:
Fag= -27.753N
Fbg= 110.253N
b)将离心力分配至轴承
平行力:Fae + Fbe=170 力矩力:Fae × 334.1+Fbe × (125-40.9)=170 × 40.9 |
求解该方程组得:
Fae= -29.376N
Fbe= 199.376N
因此,图2所示的未知矢量具有以下值(载荷)
Fa=Fag + Fae=-27.753 + (-29.376)= -57.129N
Fb=Fbg + Fbe=110.253 + 199.376=309.629N
步骤4:计算轴承寿命
由于左右两侧使用相同型号的轴承,因此使用较大的载荷数值计算其寿命。
使用公式 L=(C/P)3 × 106,将基本额定动载荷C=10094N、轴承所承受载荷P=309.629N(最大)代入公式中。
L=(10094/309.629)3 × 106=32.63 × 106=3.3 × 1010 转
因此,在本计算案例中,寿命为330亿转。
米思米 | 米思米 |
米思米 | 米思米 | 米思米 | 米思米 |
米思米 | 米思米 | ||
关联类别
· 球轴承
· 滚子轴承
· 陶瓷轴承
· 轴承组件
关联内容