下面将基于滚珠轴承的几何学讲解滚珠轴承的最高转速及其思路。
以最高转速处于同一水平的内径为φ20的滚珠轴承为例,其数据如表1所示。
表1.滚珠轴承的最高转速
分类 | 型号 | 内外径 | 最高转速 (rpm) |
深沟球轴承 | 6004 | φ20-φ42 | 18,000 |
6204 | φ20-φ47 | 16,000 | |
6304 | φ20-φ52 | 14,000 | |
角接触球轴承 | 7004 | φ20-φ42 | 19,000 |
7204 | φ20-φ47 | 17,000 | |
7304 | φ20-φ52 | 16,000 | |
圆柱滚子轴承 | NU204 | φ20-φ47 | 15,000 |
NU304 | φ20-φ52 | 13,000 |
对最高转速进行分类,可获得如下表2所示的结果。
表2.各种对比基准条件下的最大转速大小
对比基准 | 最高转速的大小 |
分类 | 圆柱滚子<深沟球<角接触球 |
外径 | Φ52<φ47<φ42 |
利于高速旋转的轴承分类为“角接触球轴承” 、外径为“φ42”。这类轴承的外圈与滚动体的接触面积大,能够以更大的面积承受滚珠因离心力而产生的载荷,从而能够降低以载荷除以面积所计算出的应力值。关于外径,外径越小则滚动体的直径越小,这样滚动体的重量就更轻,旋转产生的离心力也更小,从而使得外圈与滚动体接触所产生的应力也相应减小。角接触球轴承滚动体重量小,而离心力与重量的4次方成反比减小,因此可以实现高速旋转。
因轴承的旋转而带动滚动体旋转的转速,通过图1予以说明。
图1.旋转轴承中滚动体的运动
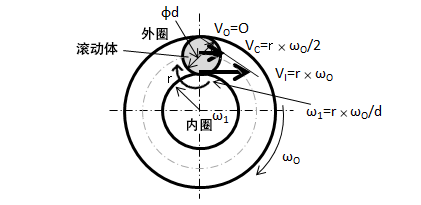
① 由于内圈在旋转,所以内圈的速度为VⅠ=r x ω0
② 由于外圈固定,所以V0=0
③ 由于滚动体是以内圈与外圈速度的一半的速度旋转,所以Vc=d/2 x ω0
这一Vc会引起滚动体的离心力,而作为其原因的加速度为:
a=Vc2/r
a:滚动体的加速度(m/s2) r:滚动体的半径(m) Vc:滚动体的速度(m/s) ω0:旋转轴的旋转速度(rad/s) ω1:滚动体的旋转速度(rad/s) d:滚动体的直径 |
代入图1所示的数字,则施加于滚动体的加速度如下所示:
a=rω02/4
可计算得出。这个数值乘以滚动体的重量后得到的数值就是所产生的离心力,滚动体的重量越小,即滚珠轴承的外径越小,离心力就越小。
米思米 | 米思米 |
米思米 | 米思米 | 米思米 | 米思米 |
米思米 | 米思米 | ||
关联类别
· 球轴承
· 滚子轴承
· 陶瓷轴承
· 轴承组件
· 润滑脂
关联内容