无油衬套负载载荷的计算示例(之1)
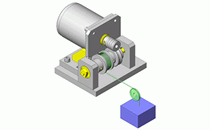
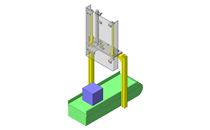
如图1所示,以滑动轴承支撑的旋转轴承所承载的负载载荷可通过如下步骤计算得出。
图1.旋转体的结构图
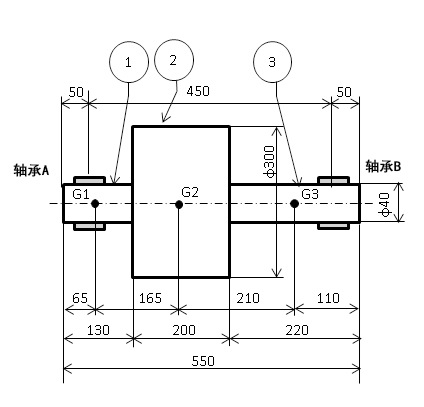
(1)计算旋转体的重量与重心位置
(2)计算轴承的负载载荷
(1)计算旋转体的重量与重心位置
表1.旋转体的质量与重心位置计算
部件 | 质量 | 重心位置 | 质量×重心位置 |
① | 1.3 | 65 | 84.5 |
② | 111.0 | 230 | 25369 |
③ | 2.2 | 440 | 968 |
部件整体 | 113.8 | 232.2*1 | 26421.5 |
注释
*1 部件整体重心位置 = 部件整体(质量×重心位置)/ 部件整体质量 = 26421.5/113.8 = 232.2mm
旋转体材质为S45C,其比重为7.8cm3。
(2)计算轴承的负载载荷
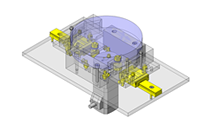
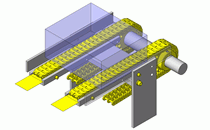
如图2所示的旋转体模型图,将施加在旋转体重心位置(GT)上的总负载载荷分配给轴承A、B,并相应计算负载载荷。
图2.旋转体的模型图
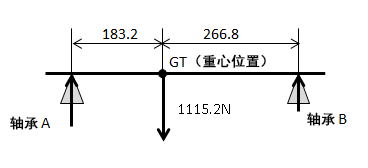
施加在轴承上的载荷可如下所示,根据以2点支撑梁上承载的集中载荷时的关系,按照以下方式计算得出。
轴承A支撑的载荷 = 1115.9 ×(266.8/450)= 67.5kgf (=661.5N)
轴承B支撑的载荷 = 1115.9 ×(183.2/450)= 46.3kgf (=453.7N)
无油衬套负载载荷的计算示例(之2)
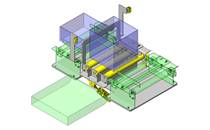
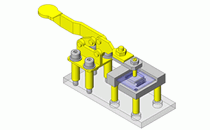
按照如下步骤,计算由图3所示的滑动轴承支撑,以1mm的偏心量安装在旋转体①上的旋转体②以1,500rpm的速度旋转时,轴承所承受的负载载荷。
图3.旋转体的结构图
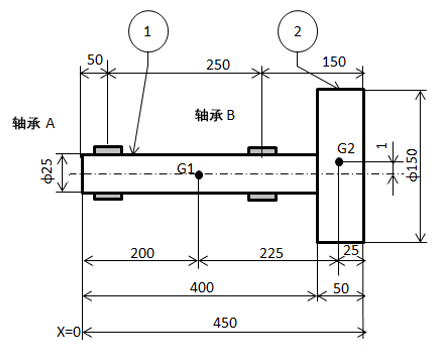
(1)计算旋转体(部件①+②)的重量与重心位置
(2)计算旋转部件②对旋转体施加的离心力
(3)计算轴承的负载载荷
(1)计算旋转体(部件①+②)的重量与重心位置
表2.旋转体的质量与重心位置计算
部件 | 质量 | 重心位置 | 质量×重心位置 |
① | 1.532 | 200 | 306.4 |
② | 6.892 | 425 | 2929.1 |
部件整体 | 8.424 | 384.1*2 | 3235.5 |
注释
*2 部件整体重心位置 = 部件整体(质量×重心位置)/ 部件整体质量 = 3235.5/8.424 = 384.1mm
旋转体材质为S45C,其比重为7.8cm3。
(2)计算旋转部件②对旋转体施加的离心力
如图3所示,由于旋转不平衡而产生的离心力作用于径向,其值可由下式计算。
此时,旋转中心与产品编号②的重心位置处的旋转轴之间的距离(偏心重心半径)为1mm。
图4.什么是离心力
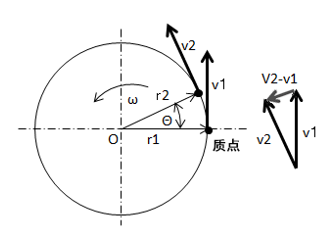
注)关于离心力 |
离心力是与重力相同的力,我们无法区分识别两者。
|
离心力计算公式:F=mrω2
F:离心力(N(kgm/s2)) m:质量(kg) r:半径(m)※偏重心半径 ω:旋转角速度(rad/s) |
将mr=6.892 × 0.001、ω=2 × π × 25代入公式中计算可得:
F = 6.892 × 0.001 × (2 × π × 25)2 = 170.1N
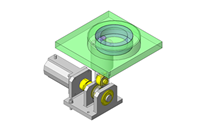
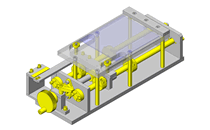
(3)计算轴承的负载载荷
图5.旋转体的模型图
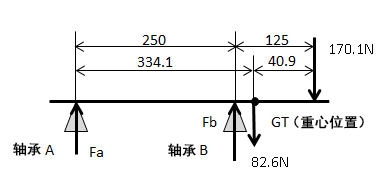
在此计算中,使用的符号如下所示。
Fag,Fbg:旋转体重量的轴承载荷 Fae,Fbe:旋转中心和产品编号②的重心位置为1mm时,因离心力而产生的轴承载荷 |
a)将作用于重心的旋转体重量分配至轴承
作用于重心的力8.424kgf(82.6N)不会产生力矩,所以可通过如下方程组计算出作用于轴承AB的力。
平行力的平衡公式:Fag + Fbg =82.6N
力矩的平衡公式:Fag× 334.1 + Fbg × 84.1= 0
Fag = -27.8N
Fbg = 110.4N
b)将偏心的产品编号②离心力分配至轴承
平行力的平衡公式:Fae + Fbe = 170.1
力矩的平衡公式:Fae × 334.1 + Fbe × 84.1 = 170.1 × 40.9
Fae = -29.4N
Fbe = 199.5N
c)计算Fa,Fb
Fa = Fag + Fae = -27.8 + (-29.4) = -57.2N
Fb = Fbg + Fbe = 110.4 + 199.5 = 309.9N
米思米 | 米思米 | 米思米 | 米思米 |
| |||
米思米 | 米思米 | 米思米 | 米思米 |
关联类别
Ø 无油衬套、垫圈
Ø 无油线性滑板
关联内容