基础系列的第5期。杠杆原理也能撬动地球吗?使用倍力机构的概要&杠杆、曲柄连杆机构、曲柄机构介绍使用事例。
· 何谓倍力机构 / 杠杆机构
· 曲柄连杆机构
· 倍力机构的使用例
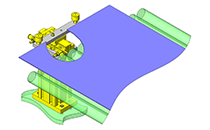
倍力机构的使用例 ① 使用杠杆的简易冲压机
简易冲压机
图5 简易冲压机的机制
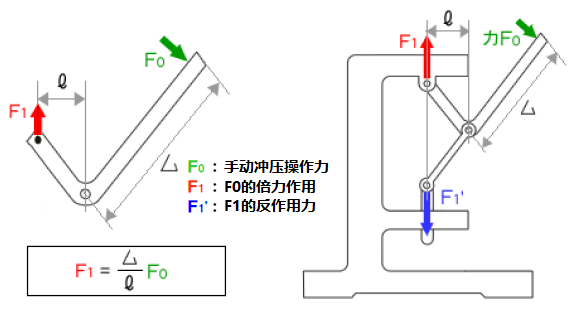
图5的机构是直角杠杆和肘节曲柄组合而成的简易冲压机。
该机构在直角杠杆的手柄部施加的力(F0),通过倍力机制可以得到与手臂长度比相应的倍力(F1),用冲压机的框体支撑该力,用肘节将其反作用力转换为相反方向并作为冲压加工力(F1’)。
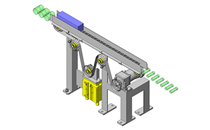
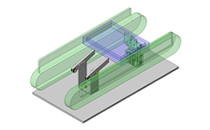
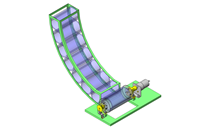
倍力机构的应用例 ② 使用曲柄和曲柄连杆机构的冲压机
冲压机的倍力机构
图6 简易概略图
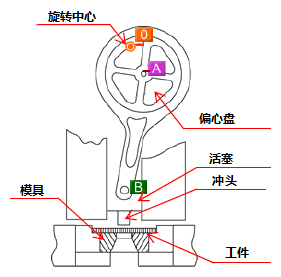
图7 矢量图
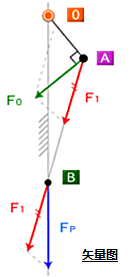
图6的机构是冲压机,该机构的曲柄OA使用偏芯盘让盘的中心(=重心)位于旋转中心O的下方时,盘的重量冲压工件的。
其中用到了曲柄和曲柄连杆机构。
图7是该机构的矢量图,可以看出通过节A和加工点B的力度的矢量比较,即可得到倍力作用。
也就是说,该机构使用偏芯盘让F0增大,并利用活塞将其转为垂直方向,从而得到冲压力Fp。
若用杠杆撬动地球,需要多长的杠杆?

“给我一个支点,我就可以撬起地球”这句话是阿基米德的名言。
那么,杠杆真的能撬动地球吗?如果可以撬动的话,需要多长的杠杆呢?我计算了一下。
假设地球的重量为5.9736 × 1024 kg, 约 6 × 1024 ,阿基米德的体重为50kg,支点到作用点的距离为1km,力点的力矩与作用点的力矩平衡的情况下,求支点到力点的距离d。
支点到力点的距离
50kg | × | d | = | 6 × 1024kg | × | 1km |
阿基米德的体重(力点上施加的力) | 支点到力点的距离 | 地球的重量 | 支点到作用点的距离 1km |
d | = | 6 × 1024 kg × 1km | = | 1.2 × 1023 km |
50kg |
若支点到力点的距离为1.2 × 1023 km,支点到作用点的距离为1km,需要的杠杆长度为120,000,000,000,000,000,000,001km。
用以1,000km/h的速度飞行的飞机移动的话,大约需要120,000,000,000,000,000,001小时。
即使假定一个人活到100岁的情况下,也需要136,986,301,000,000小时,约136兆小时,这个距离没有飞机是到达不了的。
除非人的寿命戏剧性延长,否则是不可能的。